| 2、Strat计算 | | 由于建筑外形复杂,设计单位希望导算横向应风面风荷载时,按建筑外形,不同部位按不同的体型系数导算风荷载。利用Strat的外轮廓导荷模式,很容易实现这种风荷载的导算方法。 | | 由于结构中有很多斜撑,一般按层建模的软件处理较为繁琐。利用Strat强大的三维图形功能,很容易地实现人字形斜撑、十字形斜撑、加强层钢桁架的输入。 | | 在方案计算阶段,设计单元要求考虑算裙房、和顶层的构筑物,以简化计算。 | | 据了解,设计单位用另外的软件建模时,花费时间均为一天以上。而用Strat建模时,第一花费4小时,第二次时间更少(由于方案调整较大,第二次重新建模),体现了Strat软件图形前处理的先进性。 | | | | 各软件计算的主要指标如下表所示。 |
|
| |
| | TAT | STAAD | Strat | | 总重量(万吨) | 39.5 | 34.8 | 36.7 | | 自振周期(s) | T1=6.91 | T1=6.87 | T1=6.74 | | T2=5.45 | T2=5.87 | T2=4.78 | | T3=3.95 | T3=4.47 | T3=3.35 | | 风载总荷载 (kN) | Fx=35430 | Fx=27741 | Fx=35210 | | Fy=69452 | Fy=53310 | Fy=70449 | | 地震作用 基底总剪力 (kN) | Fx=37537 | Fx=28987 | Fx=52441 | | Fy=32757 | Fy= . | Fy=49886 | | 风载 顶端侧移 (cm) | Dx= 9.65 | Dx=14.30 | Dx=11.45 | | Dy=39.58 | Dy=51.00 | Dy=51.53 | | 地震作用 顶端侧移 (cm) | Dx=13.96 | Dx=19.60 | Dx=14.96 | | Dy=26.61 | Dy=30.20 | Dy=27.57 | | | | | |
|
| 表中各指标较为分散,但大致范围还是一致的。一方面,各软件计算是分头计算,计算模型的参数不完全相同。另一方面,由于结构较为复杂,对某些特定问题,各软件的处理方法不同。如人字形斜撑、加强层斜撑,Strat释放杆端自由度按二力杆计算,其它软件则可能没有这样处理。 | | 在总重量、基本周期、地震作用顶端侧移等方面,Strat介于另两个软件之间。 | | | | 比较对于起控制作用的横向(Y向)风荷载作用: | | 1、Strat与TAT导算得到的总体风荷载相同,但TAT计算的顶端侧移小于Strat的顶端侧移(TAT/Strat=77%),表明TAT比Strat偏刚。TAT中墙单元采用的是薄壁杆模型,在一般情况下薄壁杆计算结果都偏刚(忽略了剪切变形、及其它一些假定)。 | | 2、STAAD导算得到的总体风荷载比Strat小(为Strat的76%),但计算得到的顶端侧移与Strat接近,表明STAAD的计算结果偏柔。 | | | | Strat计算结构振型如下: |
|
|
|
|
|
|
|
| | 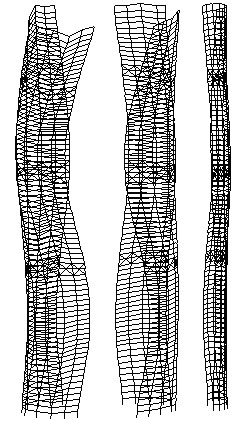
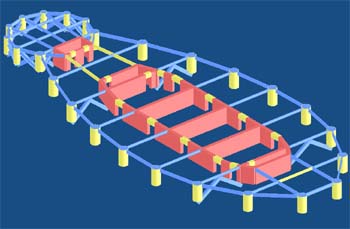
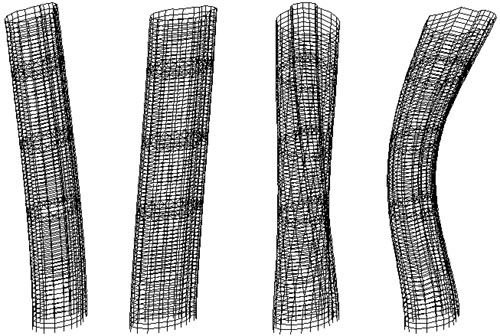
| | 从振型图上可看出,由于结构平面形状特殊,横向、扭转高阶振型呈现特殊的形态,如第8、第9、第11振型。该结构平面呈狭长形,且沿长度方向抗侧力结构类型不同:主体部分为框剪结构,端部小圆应归类为密排框筒。这两种结构类型的侧向变型形态不尽一致,且两部分之间有一定的间距,因此在具有多个反弯点的高阶振型下,这种变形差异得到放大。 |
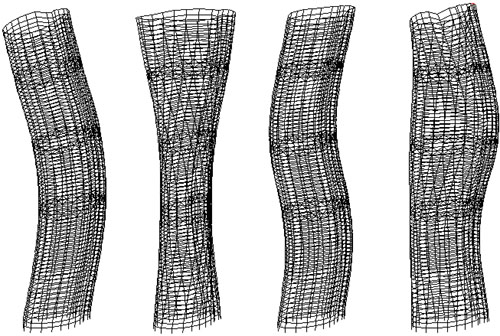
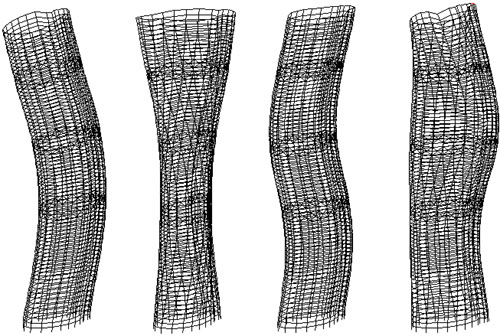
| | 为分析这种特殊振型的特点,利用Strat软件选择显示部分结构的功能,将其中的第9振型沿长度分成三个部分分别显示。如右图。从图中可看出,左端为有两个反弯点的弯曲,右端也为有两个反弯点的弯曲,但两端弯曲的方向不同,因此振型总体上仍为扭转振型。右端的弯曲幅度小于左端的弯曲幅度,因此振型呈现特殊的形态,并由此可判断该振型的扭转中心在靠近右端(端部小圆)。 |
| | | 第9振型沿平面长度方向的分解 |
|
加强层上下数层,在竖向重力恒荷载、横向(Y向)风荷载作用下的主要内力,如以下两图所示。
|
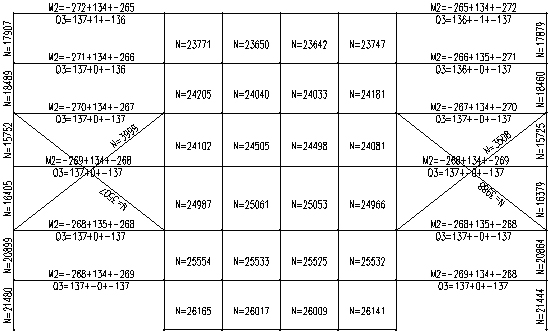
|
外伸桁架加强层在恒荷载作用下内力 |
由上图可看出,加强层外伸桁架在重力恒荷载作用下,两斜杆均为压力,且压力的大小接近。这表明,在该结构中,核心筒、外框柱在重力作用下的竖向变形协调,没有明显地通过加强层外伸桁架传力。
|
|
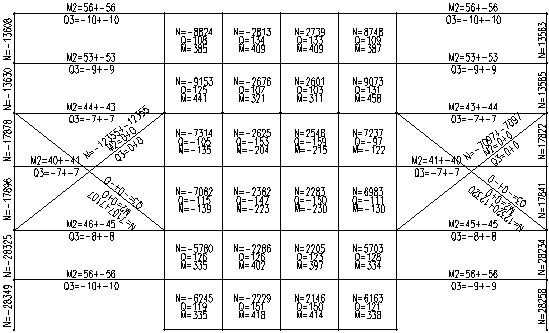
|
外伸桁架加强层在横向(Y向)风荷载作用下内力 |
| 由上图可看出,加强层外伸桁架在横向(Y向)风荷载作用下,两斜杆拉压力反号,且力的数值较大。外框柱在加强层以下轴力陡然增加,而中间墙体的总体弯矩(综合其轴力和弯矩)在加强层以下大幅减小,表明加强层能有效地将中间墙体的弯矩转化为外框柱的轴力。 |
|